File Calculator

What is the File Calculator?
How to run the File Calculator
Expressions

Groups of files
Operations and functions
Examples

Results of Inverse Solution
Results
Technical points and hints

What is the File Calculator?

This is a tool to batch-process sets of files with a mathematical expression of your liking. There can be many sets of files to use, but each set should be somehow a coherent one, f.ex. all the files of all subjects for one condition. Expressions are composed with elementary operations, see below.

How to run the File Calculator

Call the dialog from Tools | File Calculator menu.

The following dialog pops out. Fill the parameters which are relevant for you, drop the sets of files to process, then click either on the Process button:

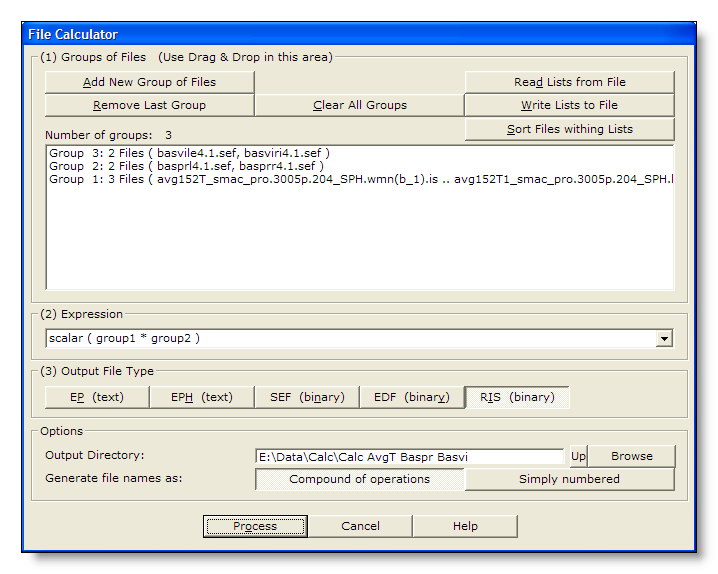
Groups of Files

You can Drag & Drop files here.

Add New Group of Files

Enter a new group of files.

See this note about groups.

Remove Last Group

Does what it says (amazing).

Clear All Groups

Clear out all the groups at once.

Read Lists from File

You can direclty retrieve the lists of groups previously saved.

Write Lists to File

You can save the lists of current groups into a file, in case you want to re-use them (much recommended!).

Sort Files within Lists

A strange behavior of Windows is to not respect the order of the files dropped in a window. To help cure this silly habit, you can sort all the file names of all the groups already entered.

Note however that Drag & Dropped files are automatically sorted.

This is an important issue, as we're going to process files in parallel between groups!

Number of Groups:

Just a counter of the number of groups entered.

Summary list of all groups

One group is displayed per line.

Expression

Enter the expression to be evaluated. Be sure you have entered all the groups needed by your expression!

Output File Type

EP (text)

Text file, see the .ep file specification.

EPH (text)

Text file, see the .eph file specification.

SEF (binary)

Binary file, see the .sef file specification.

Compact format which can handle all the basic informations for EEG.

EDF (binary)

Binary file, see the .edf file specification.

Useful only for data interchange, otherwise don't use (loss of precision)!

RIS (binary)

Binary file, see the .ris file specification.

Produced by the matrix multiplication / Inverse Solution computation.

Options

Output Directory

What it says: where to put the results!

Generate file names as:

Compound of Operations

Each file name will hold a condensed version of the operations applied from the originals. See this note.

Use this if you want to remember precisely what are your files, f.ex. for Inverse Solutions. Be aware that too many operations will generate very long and unreadible file names, and can even crash Cartool.

Simply Numbered

Just generate file names as a numbered list. See this note.

Process

Run the batch processing.

The button remains disabled until all parameters are OK.

Cancel

Quit the dialog.

Help

Launch the Help to the right page (should be here...).

Expressions

You have to provide a mathematical expression to be applied on your files.

First understand what is meant by groups of files, then see what operations can be applied to them.

Groups of files

Operands are usually whole sets of files, and each set should have some coherence of its own :

Having some sort of semantic associated to it, f.ex. all the subjects for 1 condition, or all the epochs of 1 subject etc...
Having the same number of electrodes / solution points & same number of time frames among files.
Preferably files being of the same types, i.e. not mixing scalar and vector values.
Preferaby files having the same extensions, but not mandatory.

Among groups, however, sizes and types can differ. However a given operation should receive compatible groups, f.ex.:

Summing, subtracting etc... between 2 groups: both groups should have the same number of electrodes, time frames, and number of files.
Multiplying matrices with EEG: the usual Line / Column dimensions criterion should be satisfied.

Groups are used by sequentially and synchronically processing each of their files , f.ex. summing all the files of two groups:

Group1

Group2

"+" operation

cond1.subj1

cond2.subj1

cond1.subj1 + cond2.subj1

cond1.subj2

cond2.subj2

cond1.subj2 + cond2.subj2

cond1.subj3

cond2.subj3

cond1.subj3 + cond2.subj3

...

...

...

cond1.subjn

cond2.subjn

cond1.subjn + cond2.subjn

Matrix multiplication, though, is a special case. One matrix is taken, then all the EEG are multiplied to it, then the next matrix, and so on:

Group1

Group2

"*" operation

matrix1

subj1
subj2
subj3
...
subjn

matrix1 * subj1
matrix1 * subj2
matrix1 * subj3
...
matrix1 * subjn

matrix2

subj1
subj2
subj3
...
subjn

matrix2 * subj1
matrix2 * subj2
matrix2 * subj3
...
matrix2 * subjn

...

...

...

matrixm

subj1
subj2
subj3
...
subjn

matrixm * subj1
matrixm * subj2
matrixm * subj3
...
matrixm * subjn

Operations & functions available

Group, Group1, Group2... are groups of files.
Value is a scalar value.
Vector3D is a 3D vector (x, y, z).

Operation & operands

Description

Type of results

Group + Value
Value + Group

Add a constant value to a group of files.
Input files should contain scalar values.

Group,
scalar values

Group + Vector3D

Add a constant vector to a group of files.
Input files should contain 3D vectors.

Group,
3D vectors

Group1 + Group2

Sum all files of Group1 with the files of Group2.
Input files should both contain either scalar values or 3D vectors, but not a mix of the two.

Group,
scalar values if input are scalar values,
3D vectors if input are 3D vectors

Group - Value

Subtract a constant value to a group of files.
Input files should contain scalar values.

Group,
scalar values

Group - Vector3D

Subtract a constant vector to a group of files.
Input files should contain 3D vectors.

Group,
3D vectors

Group1 - Group2

Subtract all files of Group1 with the files of Group2.
Input files should both contain either scalar values or 3D vectors, but not a mix of the two.

Group,
scalar values if input are scalar values,
3D vectors if input are 3D vectors

Group * Value
Value * Group

Multiply the group of files by a constant value.
Input files could contain either scalar values or 3D vectors.

Group,
scalar values if input are scalar values,
3D vectors if input are 3D vectors

Group1 * Group2

Multiply all files from Group1 by the files of Group2.
Group1 should contain matrices.
Group2 should contain files of 2D data, like EEG.

Group,
scalar values or 3D vectors according to each matrix

Group / Value

Divide the group of files by a constant value.
Input files could contain either scalar values or 3D vectors.

Group,
scalar values if input are scalar values,
3D vectors if input are 3D vectors

Function & operands

Description

Type of results

Abs ( Group )

Input files are scalar values: absolute values.
Input files are 3D vectors: norm of the vectors.

Group,
scalar values

Scalar ( Group )

Input files are scalar values: values untouched.
Input files are 3D vectors: norm of the vectors.

Group,
scalar values

Sqr ( Group )

Input files are scalar values: the square of the values.
Input files are 3D vectors: square of the norm of the vectors.

Group,
scalar values

Sqrt ( Group )

Input files are scalar values: the square root of the values.
Input files are 3D vectors: not allowed.

Group,
scalar values

Examples of expressions

Group1

Handy to just rename a bunch of files, and / or convert format. Check Simply Numbered from the Generate file names option.

Group1 * Group2

Compute the results of Inverse Solutions, if Group1 holds the matrices and Group2 the EEG.
Outputted .ris files can be either scalar or vectorial.

See the next paragraph for more on IS.

Group1 - Group2

Compute the differences between two sets of files.
This could be either 2 EEGs or 2 results from Inverse Solution. In the last case, they can correctly be either of scalar or vectorial types.

( 3 * Group1 + 2 * Group2 ) / 5

Do a weighted sum of two groups.
Groups can be either scalars or vectorials.

Computing "Results of Inverse Solutions"

!New!

It is now strongly recommended to use the new dedicated tool to compute the results of inverse solutions .

This tool offers much more controls over this process, like preprocessing filter, postprocessing standardization, per group average etc... It also performs numerous consistency checks on all the input files, so the results are also safer.

Use that tool - now.

The old way - if you really insist:

You can use the File Calculator to produce the final stage of the Inverse Solution, what we call Results of Inverse Solution, or RIS (see .ris files). Provided one or more matrix(ces) of Inverse Solution , you can batch this computation according to your needs.

To see how you can compute the inverse matrices, go here, and to see how you can use these matrices for display, go here.

Say we dropped the matrices into Group1, and some ERPs for two conditions into Group2 and Group3 respectively. Here are the most common options to compute the results of inverse solutions (which one is "the right one" depends on your experiment, paradigm and tests):

Group1 * Group2

and

Group1 * Group3

Multiplying the matrices by the EEGs is the basic operation.

The resulting files can either hold vectors (the most common cases) or scalar values for each solution points location, which is quite important to know for your next steps (usually, statistics).

Scalar ( Group1 * Group2 )

and

Scalar ( Group1 * Group3 )

We can add a step to the multiplication, by forcing the results to be scalar values.

If the results of the multiplication are vectors, the Scalar operation will convert them to their (Euclidian) norm. This is the same as the Abs function.

If the results of the multiplication are already scalars, the Scalar operation will do nothing. This is not the same as the Abs function, as the Abs will remove the sign of the scalar values, which Scalar does preserve.

Group1 * ( Group2 - Group3 )

or

Group1 * Group2 - Group1 * Group3

We can compute the difference in the inverse solution space between the two conditions. The two formula are mathematically equivalent, though the former is faster (2 operations, and only one multiplication).

This formula accounts for the directions of the vectors in the inverse space: vectors are being subtracted between the 2 conditions.

Abs ( Group1 * ( Group2 - Group3 ) )

or

Abs ( Group1 * Group2 - Group1 * Group3 )

Same as above, then converting to the absolute / norm values. We end up with the intensity of the vectorial differences between the two conditions.

Scalar ( Group1 * Group2 )
- Scalar ( Group1 * Group3 )

For vectorial inverse, this computes the difference of intensities between the two conditions, without accounting whatsoever with the directions of the vectors.

For scalar inverse, this computes the difference of (signed) values between the two conditions

Results are signed scalar values (positive and negative).

Abs ( Scalar ( Group1 * Group2 )
- Scalar ( Group1 * Group3 ) )

Same as above, then converting all differences into positive values.

Abs ( Abs ( Group1 * Group2 )
- Abs ( Group1 * Group3 ) )

We compute here the difference of absolute intensities between the two conditions (without, for the vectorial inverse, accounting whatsoever for the directions of the vectors).

Results are positive scalar values.

Abs ( Sqr ( Group1 * Group2 )
- Sqr ( Group1 * Group3 ) )

Just a variation of the previous formula, giving the absolute difference of powers between the two conditions.

File Calculator - Results

Processed files are written in the base directory. File names can be either a compound of the applied operations, or a simple numbered list of files based on the base directory name. Extension is the one specified in the paramaters.
The type of results will depend on what you asked for, f.ex. it is usually scalar values ("numbers"), but it can be vectors, as from the Inverse Solution computation.
The dimensions of the results also depends on the operations applied, so they can have different sizes as compared to the input files.
Verbose file .vrb (text), showing all the parameters.

File Calculator - Technical points and hints

Output file names

By default, Cartool will generate file names that reflect the whole set of operations. These are not exact replicas of the expression, but rather a construction derived of it. This is meant to help remember what operations have been done on the files.

To do so, it will use the original file names, insert the operators / functions used one at a time, then optinally shrink the resulting file names if they appear to be too long. F.ex.:

Expression Group1 - Group2 can generate basprr4-basviri4.eph
Expression Scalar ( Group1 * ( Group2 - Group3 ) ) can generate Scalar(Avg152tSmacProSph.lorb1.basprr4-basviri4).ris

One problem arises with operator like * / and the like, which Windows does not want at all in file names. In these cases, a "." (dot) is used instead of the operator.

If not a compound of operations, file names will simply repeat the last directory part of the Base Directory, then add an index value, f.ex.:

Calc G1-G2.0001.eph
Calc G1-G2.0002.eph
Calc G1-G2.0003.eph
etc...

Disk space

All these operations will use the disk to store the temporary and the final results. There is no way to do otherwise, as you know, this is a batch tool! Plus you can process gigabytes of data.

Consequently, think of having some significant room left on your hard drive ! The more elaborated your expression, the more space you need, but as a rule of thumb, say you need 3 times the amount of data you process in free space (if data are already in binary format, otherwise, maybe 2 times should be fine).

Errors

Some errors in your expression can be detected when you start the processing, like missing parenthesis, missing operands and the like.

But some other errors will be only be found when reaching the problematic part, like wrong types of operands (adding vectors to scalars).

Groups of Files	You can Drag & Drop files here.
Add New Group of Files	Enter a new group of files. See this note about groups.
Remove Last Group	Does what it says (amazing).
Clear All Groups	Clear out all the groups at once.
Read Lists from File	You can direclty retrieve the lists of groups previously saved.
Write Lists to File	You can save the lists of current groups into a file, in case you want to re-use them (much recommended!).
Sort Files within Lists	A strange behavior of Windows is to not respect the order of the files dropped in a window. To help cure this silly habit, you can sort all the file names of all the groups already entered. Note however that Drag & Dropped files are automatically sorted. This is an important issue, as we're going to process files in parallel between groups!

Number of Groups:	Just a counter of the number of groups entered.
Summary list of all groups	One group is displayed per line.

Expression	Enter the expression to be evaluated. Be sure you have entered all the groups needed by your expression!

Output File Type
EP (text)	Text file, see the *.ep* file specification.
EPH (text)	Text file, see the *.eph* file specification.
SEF (binary)	Binary file, see the *.sef* file specification. Compact format which can handle all the basic informations for EEG.
EDF (binary)	Binary file, see the *.edf* file specification. Useful only for data interchange, otherwise don't use (loss of precision)!
RIS (binary)	Binary file, see the *.ris* file specification. Produced by the matrix multiplication / Inverse Solution computation.

Options
Output Directory	What it says: where to put the results!
Generate file names as:
Compound of Operations	Each file name will hold a condensed version of the operations applied from the originals. See this note. Use this if you want to remember precisely what are your files, f.ex. for Inverse Solutions. Be aware that too many operations will generate very long and unreadible file names, and can even crash Cartool.
Simply Numbered	Just generate file names as a numbered list. See this note.

Process	Run the batch processing. The button remains disabled until all parameters are OK.
Cancel	Quit the dialog.
Help	Launch the Help to the right page (should be here...).

Group1	Group2	"+" operation
cond1.subj1	cond2.subj1	cond1.subj1 + cond2.subj1
cond1.subj2	cond2.subj2	cond1.subj2 + cond2.subj2
cond1.subj3	cond2.subj3	cond1.subj3 + cond2.subj3
...	...	...
cond1.subjn	cond2.subjn	cond1.subjn + cond2.subjn

Group1	Group2	*"" operation**
matrix1	subj1 subj2 subj3 ... subjn	matrix1 * subj1 matrix1 * subj2 matrix1 * subj3 ... matrix1 * subjn
matrix2	subj1 subj2 subj3 ... subjn	matrix2 * subj1 matrix2 * subj2 matrix2 * subj3 ... matrix2 * subjn
...	...	...
matrixm	subj1 subj2 subj3 ... subjn	matrixm * subj1 matrixm * subj2 matrixm * subj3 ... matrixm * subjn

Operation & operands	Description	Type of results

Group + Value Value + Group	Add a constant value to a group of files. Input files should contain scalar values.	Group, scalar values
Group + Vector3D	Add a constant vector to a group of files. Input files should contain 3D vectors.	Group, 3D vectors
Group1 + Group2	Sum all files of Group1 with the files of Group2. Input files should both contain either scalar values or 3D vectors, but not a mix of the two.	Group, scalar values if input are scalar values, 3D vectors if input are 3D vectors

Group - Value	Subtract a constant value to a group of files. Input files should contain scalar values.	Group, scalar values
Group - Vector3D	Subtract a constant vector to a group of files. Input files should contain 3D vectors.	Group, 3D vectors
Group1 - Group2	Subtract all files of Group1 with the files of Group2. Input files should both contain either scalar values or 3D vectors, but not a mix of the two.	Group, scalar values if input are scalar values, 3D vectors if input are 3D vectors

*Group Value Value * Group**	Multiply the group of files by a constant value. Input files could contain either scalar values or 3D vectors.	Group, scalar values if input are scalar values, 3D vectors if input are 3D vectors
*Group1 Group2**	Multiply all files from Group1 by the files of Group2. Group1 should contain matrices. Group2 should contain files of 2D data, like EEG.	Group, scalar values or 3D vectors according to each matrix

Group / Value	Divide the group of files by a constant value. Input files could contain either scalar values or 3D vectors.	Group, scalar values if input are scalar values, 3D vectors if input are 3D vectors

Function & operands	Description	Type of results

Abs ( Group )	Input files are scalar values: absolute values. Input files are 3D vectors: norm of the vectors.	Group, scalar values

Scalar ( Group )	Input files are scalar values: values untouched. Input files are 3D vectors: norm of the vectors.	Group, scalar values

Sqr ( Group )	Input files are scalar values: the square of the values. Input files are 3D vectors: square of the norm of the vectors.	Group, scalar values

Sqrt ( Group )	Input files are scalar values: the square root of the values. Input files are 3D vectors: not allowed.	Group, scalar values

Group1	Handy to just rename a bunch of files, and / or convert format. Check Simply Numbered from the Generate file names option.
*Group1 Group2**	Compute the results of Inverse Solutions, if Group1 holds the matrices and Group2 the EEG. Outputted *.ris* files can be either scalar or vectorial. See the next paragraph for more on IS.
Group1 - Group2	Compute the differences between two sets of files. This could be either 2 EEGs or 2 results from Inverse Solution. In the last case, they can correctly be either of scalar or vectorial types.
*( 3 Group1 + 2 * Group2 ) / 5**	Do a weighted sum of two groups. Groups can be either scalars or vectorials.

*Group1 Group2 and Group1 * Group3**	Multiplying the matrices by the EEGs is the basic operation. The resulting files can either hold vectors (the most common cases) or scalar values for each solution points location, which is quite important to know for your next steps (usually, statistics).

*Scalar ( Group1 Group2 ) and Scalar ( Group1 * Group3 )**	We can add a step to the multiplication, by forcing the results to be scalar values. If the results of the multiplication are vectors, the Scalar operation will convert them to their (Euclidian) norm. This is the same as the Abs function. If the results of the multiplication are already scalars, the Scalar operation will do nothing. This is not the same as the Abs function, as the Abs will remove the sign of the scalar values, which Scalar does preserve.

*Group1 ( Group2 - Group3 ) or Group1 * Group2 - Group1 * Group3**	We can compute the difference in the inverse solution space between the two conditions. The two formula are mathematically equivalent, though the former is faster (2 operations, and only one multiplication). This formula accounts for the directions of the vectors in the inverse space: vectors are being subtracted between the 2 conditions.
*Abs ( Group1 ( Group2 - Group3 ) ) or Abs ( Group1 * Group2 - Group1 * Group3 )**	Same as above, then converting to the absolute / norm values. We end up with the intensity of the vectorial differences between the two conditions.
*Scalar ( Group1 Group2 ) - Scalar ( Group1 * Group3 )**	For vectorial inverse, this computes the difference of intensities between the two conditions, without accounting whatsoever with the directions of the vectors. For scalar inverse, this computes the difference of (signed) values between the two conditions Results are signed scalar values (positive and negative).
*Abs ( Scalar ( Group1 Group2 ) - Scalar ( Group1 * Group3 ) )**	Same as above, then converting all differences into positive values.
*Abs ( Abs ( Group1 Group2 ) - Abs ( Group1 * Group3 ) )**	We compute here the difference of absolute intensities between the two conditions (without, for the vectorial inverse, accounting whatsoever for the directions of the vectors). Results are positive scalar values.
*Abs ( Sqr ( Group1 Group2 ) - Sqr ( Group1 * Group3 ) )**	Just a variation of the previous formula, giving the absolute difference of powers between the two conditions.